How to Continuously Move in 2048
Updates
2017-09-25 There was some lively discussion about this series on Hacker News.
This post is the first in a series. Next: Counting States with Combinatorics.

As part of a recent revamp, 2048's "You win!" screen started reporting the number of moves it took to win, which made me wonder: how many moves should it take to win?
In this post, we'll answer that question by modeling the game of 2048 as a Markov chain and analyzing it to show that, no matter how well the player plays, the number of moves required to win the game is at least 938.8 on average. This gives us a benchmark — if you can win in around this number of moves, you're doing pretty well.
The number of moves needed to win depends on random chance, because the game adds 2 and 4 tiles at random. The analysis will also show that the distribution for the minimum number of moves to win has a standard deviation of 8.3 moves, and that its overall shape is well-approximated by a mixture of binomial distributions.
To obtain these results, we'll use a simplified version of 2048: instead of placing the tiles on a board, we'll… throw them into a bag. That is, we'll ignore the geometric constraints imposed by the board on which tiles can be merged together. This simplification makes our job much easier, because the player no longer has to make any decisions 1, and because we don't have to keep track of where the tiles are on the board.
The price we pay for relaxing the geometric constraints is that we can only compute a lower bound on the expected number of moves to win; it might be that the geometric constraints make it impossible to attain that bound. However, by playing many games of 2048 (for science!), I'll also show that we can often get close to this lower bound in practice.
If you're not familiar with 2048 or with Markov chains, that's OK — I'll introduce the necessary ideas as we go. The (research quality) code behind this article is open source, in case you'd like to see the code to generate the chain and the plots.
2048 as a Markov Chain
To represent our simplified '2048 in a bag' game as a Markov chain, we need to define the states and the transition probabilities of the chain. Each state is like a snapshot of the game at a moment in time, and the transition probabilities specify, for each state, which state is likely to come next.
Here we will define each state to encode which tiles are currently in the bag. We don't care about the order of the tiles, so we can think of it as a multiset of tiles. Initially, there are no tiles, so our initial state is simply the empty set. In diagram form, which we'll add to below, this initial state looks like:
Setting up the Board

A sample of a dozen new game boards.
When we start a new game of 2048, the game places two random tiles on the board (see examples above). To represent this in the Markov chain, we need to work out the transition probabilities from the initial state to each of the possible successor states.
Fortunately, we can look at the game's source code to find out how the game does this. Whenever the game places a random tile on the board, it always follows the same process: pick an available cell uniformly at random, then add a new tile either with value 2, with probability 0.9, or value 4, with probability 0.1.
For 2048 in a bag, we don't care about finding an available cell, because we haven't put any capacity constraint on the bag; we just care about adding either a 2 or 4 tile with the given probabilities. This leads to three possible successor states for the initial state:
- \(\{2, 2\}\) when both of the new tiles are
2s. This happens with probability \(0.9 \times 0.9 = 0.81\). - \(\{4, 4\}\) when both of the new tiles are
4s. This happens with probability \(0.1 \times 0.1 = 0.01\) — that is, you are pretty lucky if you start with two4s. - \(\{2, 4\}\) when the new tiles are
2and then4, which happens with probability \(0.9 \times 0.1 = 0.09\), or4and then2, which happens with probability \(0.1 \times 0.9 = 0.09\). We don't care about order, so both cases lead to the same state, with total probability \(0.09 + 0.09 = 0.18\).
We can add these successor states and their transition probabilities to the Markov chain diagram as follows, where the transition probabilities are written on the edge labels, and the new nodes and edges are shown in blue:
Playing the Game
With the first pair of tiles now placed, we're ready to start playing the game. In the real game, this means that the player gets to swipe left, right, up or down to try to bring pairs of like tiles together. In the bag game, however, there is nothing to stop us from merging all pairs of like tiles, so that's what we'll do.
In particular, the rule for merging tiles in the bag game is: find all of the pairs of tiles in the bag that have the same value and remove them; then replace each pair of tiles with a single tile with twice the value 2.
Once pairs of like tiles have been merged, the game adds a single new tile at random using the same process as above — that is, a 2 tile with probability 0.9, or a 4 tile with probability 0.1 — to arrive at the successor state.
For example, to find the possible successors of the state \(\{2, 2\}\), we first merge the two 2 tiles into a single 4 tile, and then the game will add either a 2 tile or a 4 tile. The possible successors are therefore \(\{2, 4\}\) and \(\{4, 4\}\), which, as it happens, we have already encountered. The diagram including these two transitions from \(\{2, 2\}\), which have probability 0.9 and 0.1 respectively, is then:
If we follow the same process for the successors of \(\{2, 4\}\), we see that no merging is possible yet, because there is no pair of like tiles, and the successor state will either be \(\{2, 2, 4\}\) or \(\{2, 4, 4\}\), depending on whether the new tile is a 2 or 4. The updated diagram is then:
Layers and 'Skipping'
We can continue adding transitions in this way. However, as we add more states and transitions, the diagrams can become quite complicated 3. We can make the diagrams a bit more orderly by using the following observation: the sum of the tiles in the bag increases by either 2 or 4 with each transition. This is because merging pairs of like tiles does not change the sum of the tiles in the bag (or on the board — this property also holds in the real game), and the game always adds either a 2 tile or a 4 tile.
If we group states together into 'layers' by their sum, the first few layers look like this:
For later layers, I've also omitted the labels for transitions with probability 0.9 (solid lines, unless otherwise labelled) and 0.1 (dashed lines), to reduce clutter.
Grouping the states into layers by sum makes another pattern clear: each transition (other than those from the initial state) is either to the next layer, with probability 0.9, or the layer after, with probability 0.1. (This is particularly clear if you look at the layers with sums 8, 10 and 12 in the diagram above.) That is, most of the time the game gives us a 2, and we'll transition to the next layer, but sometimes we get lucky, and the game gives us a 4, which means we get to skip a layer, getting us slightly closer to our goal of reaching the 2048 tile.
The End Game
We could continue this process forever, but since we are only interested in reaching the 2048 tile, we'll stop it at that point by making any state with a 2048 tile an absorbing state. An absorbing state has a single transition, which is to itself with probability 1 — that is, once you reach an absorbing state, you can never leave.
In this case all of the absorbing states are 'win states' — you have a 2048 tile and have therefore won the game. There is no way to 'lose' the bag game, because unlike in the real game, we cannot get into a situation where the board (or bag) is full.
The first state that contains a 2048 tile is in the layer with sum 2066. It's notable that you can't get a 2048 tile on its own on the board — it takes a few moves to merge the 1024 tiles, the 512 tiles, and so on, during which you accumulate more 2 and 4 tiles. This is why the sum of the tiles for the first state with a 2048 tile is higher than 2048.
Here's what the graph looks like around this first winning state (see more), with the absorbing states colored red:
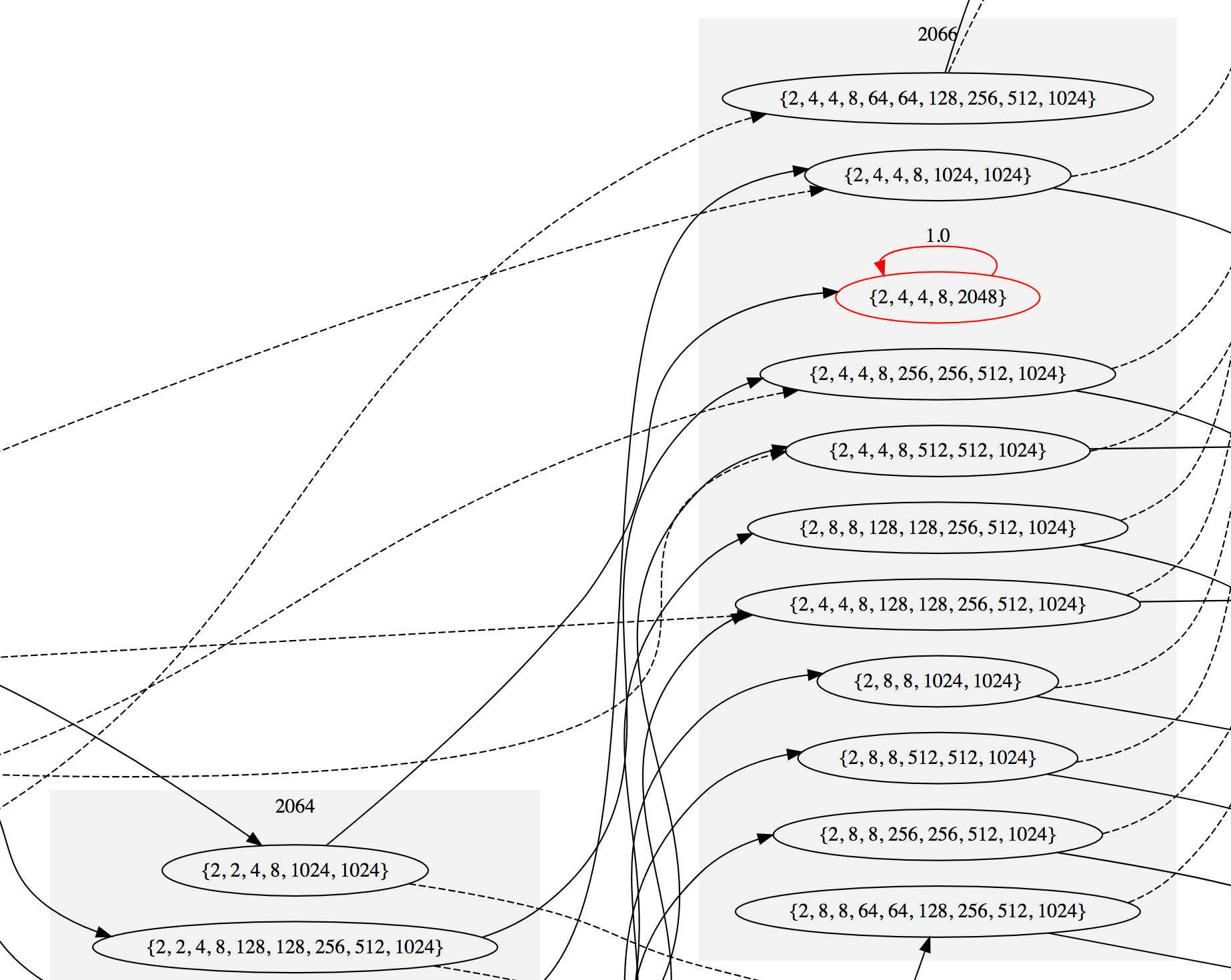
If we continue to add transitions until there are no non-absorbing states left, we eventually end up with 3487 states, of which 26 are absorbing; this completes the definition of the Markov chain. The diagram for the full chain is quite large, but if your device can handle a 5MB SVG file, here is a diagram of the full chain (you may need to scroll down a bit to see the start). When very zoomed out, it looks like this:

Sampling from the Chain
Now that we have put in the effort to model 2048 (in a bag) as a Markov chain, the simplest way to find out how many moves it takes before we are absorbed is to run simulations. In each simulation, we generate a single trajectory through the chain by starting at the initial state, then choosing a successor state at random in proportion to the transition probabilities, then repeating from that state. After one million simulation runs, the following distribution emerges for the number of moves to win:
The mean, which is marked by the vertical blue line, comes out at 938.8 moves, excluding the first transition from the initial state, with a standard deviation of 8.3 moves. So, that's our answer for the minimum expected number of moves to win the game!
The theory of Markov chains also lets us calculate some of these properties directly using clever mathematics. In Appendix A, I'll show how to calculate the mean and standard deviation for the number of moves without relying on simulation. Then, in Appendix B, I'll use some of properties of the chain to offer at least a partial explanation of the shape of the distribution.
Putting Theory to the Test
Finally, to test these results in real life, I played a lot of 2048 (for science!) and, for the 28 games I won, recorded the number of moves it took and also the sum of the tiles on the board when I reached the 2048 tile 4:
Transcribing these numbers into a spreadsheet and plotting them leads to the following scatter plot:
I've marked the minimum expected number of moves, plus or minus one standard deviation, in blue, and the tile sum 2066, which we found to be the lowest sum of tiles for which it was possible to have a 2048 tile, in red.
The sum of the tiles on the board is important, because when it's large, that typically means that I made a mistake that left a large tile stranded somewhere I could not merge it with any other tile. It then took many more moves to build up that tile again in a place where it could be merged (or to set up the board to try to get into the right place to merge) with another large tile.
If I were very good at playing 2048, we'd predict my results would cluster in the bottom left corner of the graph, and that most of them would lie between the dashed blue lines. In fact, we see that, while I sometimes get close to this ideal, I am not very consistent — there are plenty of points in the top right, with lots of extra moves and extra tiles.
This plot also highlights the fact that this analysis gives us only the minimum expected number of moves. There were a few games where I got lucky and won in less than 938.8 moves, including one win with 927 moves and a tile sum of 2076. (It is the second from the left in the bottom row of the montage above.) This is essentially because I got a lot of 4 tiles in that game, just by chance, and also because I didn't make any major blunders that required extra moves.
In principle, there is non-zero probability that we could win the game in only 519 moves. We can find this by walking through the chain, always taking the transition for the 4, and counting the number of transitions required to reach a 2048 tile. However, the probability of this occurring is \(0.1^{521}\), or \(10^{-521}\); there are only about \(10^{80}\) atoms in the observable universe, so you shouldn't hold your breath waiting for such a game to happen to you. Similarly, if we are very unlucky and always get 2 tiles, we should still be able to win in only 1032 moves. Such a game is much more likely, with a probability of \(0.9^{1034}\), which is about \(10^{-48}\), but you probably shouldn't hold your breath waiting for that game either. The average of 938.8 moves is much closer to 1032 than 519, because 2 tiles are much more likely than 4 tiles.
Conclusion
In this post we have seen how to construct a Markov chain that models how a game of 2048 evolves if it is always possible to merge like tiles. By doing so, we've been able to apply techniques from the theory of absorbing Markov chains to calculate interesting properties of the game, and in particular that it takes at least 938.8 moves to win, on average.
The main simplification that enabled this approach was to ignore the structure of the board, effectively assuming that we threw tiles into a bag, rather than placing them onto the board. In my next post, I plan to look at what happens when we do consider the structure of the board. We'll see that the number of states we need to consider becomes many orders of magnitude larger (though perhaps not as large as one might think), and also that we will need to leave the world of Markov chains and enter the world of Markov Decision Processes, which allow us to bring the player back into the equation, and in principle may allow us to 'solve' the game completely — to find a provably optimal way of playing.
Appendix A: Analysis of the Markov Chain
Once that we've defined our Markov chain, we can bring some powerful mathematical machinery to bear to calculate its properties without simulation. Many of these calculations are possible only because our Markov chain is a special type of Markov chain called an absorbing Markov chain.
The criteria for being an absorbing Markov chain are that:
-
There must be at least one absorbing state. As we've seen above, there are 26 absorbing states, one for each winning state with a
2048tile. -
For any state, it is possible to reach an absorbing state in a finite number of transitions. One way to see that this holds for our chain is to observe that there are no loops other than for the absorbing states — except for the absorbing states, the chain is a directed acyclic graph.
The Transition Matrix
Now that we have established that we have an absorbing Markov chain, the next step is to write out its transition matrix in canonical form. A transition matrix is a matrix that organizes the transition probabilities, which we defined for our chain above, such that the \((i, j)\) entry is the probability of transitioning from state \(i\) to state \(j\).
For the transition matrix, \(\mathbf{P}\), of an absorbing chain with \(r\) absorbing states and \(t\) transient (which means non-absorbing) states, to be in canonical form, it must be possible to break it up into four smaller matrices, \(\mathbf{Q}\), \(\mathbf{R}\), \(\mathbf{0}\) and \(\mathbf{I}_r\), such that: \[ \mathbf{P} = \left( \begin{array}{cc} \mathbf{Q} & \mathbf{R} \\\
\mathbf{0} & \mathbf{I}_r \end{array} \right) \] where \(\mathbf{Q}\) is a \(t \times t\) matrix that describes the probability of transitioning from one transient state to another transient state, \(\mathbf{R}\) is a \(t \times r\) matrix that describes the probability of transitioning from a transient state to an absorbing state, \(\mathbf{0}\) denotes an \(r \times t\) matrix of zeros, and \(\mathbf{I}_r\) is the transition matrix for the absorbing states, which is an \(r \times r\) identity matrix.
To get a transition matrix in canonical form for our chain, we need to decide on an ordering of the states. It suffices to order states (1) by whether they are absorbing, with absorbing states last, then (2) by the sum of their tiles, in ascending order, and finally (3) in lexical order, to break ties. If we do this, we obtain the following matrix:
It's quite large, namely \(3487 \times 3487\), so when zoomed out it just looks pretty much diagonal, but if we zoom in on the lower right hand corner, we can see that it does have some structure, and in particular it has the canonical form that we're after:
The Fundamental Matrix
With the transition matrix in canonical form, the next step is to use it to find what is called the fundamental matrix for the chain, which will let us calculate the expected number of transitions before absorption, which is (finally!) the answer to our original question.
The fundamental matrix, \(\mathbf{N}\), is defined in terms of \(\mathbf{Q}\) by the identity \[ \mathbf{N} = \sum_{k=0}^{\infty} \mathbf{Q}^k \] where \(\mathbf{Q}^k\) denotes the \(k\)th matrix power of \(\mathbf{Q}\).
The \((i, j)\) entry of \(\mathbf{N}\) has a particular interpretation: it is the expected number of times that we would enter state \(j\) if we followed the chain starting from state \(i\). To see this, we can we observe that, just as the \((i, j)\) entry of \(\mathbf{Q}\) is the probability of transitioning from state \(i\) to state \(j\) in a single transition, the \((i, j)\) entry of \(\mathbf{Q}^k\) is the probability of entering state \(j\) exactly \(k\) transitions after entering state \(i\). If, for a given pair of states \(i\) and \(j\), we add up said probabilities for all \(k \geq 0\), the summation includes every time at which we could possibly enter state \(j\) after state \(i\), weighted by the corresponding probability, which is what gives us the desired expectation.
Fortunately, the fundamental matrix can also be calculated directly, without the awkward infinite summation, as the inverse of the matrix \(\mathbf{I}_t - \mathbf{Q}\), where \(\mathbf{I}_t\) is the \(t \times t\) identity matrix; that is, \(\mathbf{N} = (\mathbf{I}_t - \mathbf{Q})^{-1}\). (The proof of this identity is left as an exercise for the reader!)
Expected Moves to Win
Once we have the fundamental matrix, we can find the expected number of transitions from any state \(i\) to an absorbing state by summing up all of the entries in row \(i\) — in other words, the number of transitions before we reach an absorbing state is the total number of transitions that we spend in all of the transient states along the way.
We can obtain these row sums for all states at once by calculating the matrix-vector product \(\mathbf{N} \mathbf{1}\), where \(\mathbf{1}\) denotes a column vector of \(t\) ones. Since \(\mathbf{N} = (\mathbf{I}_t - \mathbf{Q})^{-1}\), we can do this efficiently by solving the linear system of equations \[ (\mathbf{I}_t - \mathbf{Q})\mathbf{t} = \mathbf{1} \] for \(\mathbf{t}\). The entry in \(\mathbf{t}\) that corresponds to the initial state (the empty set, \(\{\}\)) is the number of transitions. In this case, the number that comes out is 939.8. To finish up, we just need to subtract \(1\), because the transition from the initial state doesn't count as a move. This gives our final answer as 938.8 moves.
We can also obtain the variance for the minimum number of moves as \( 2(\mathbf{N} - \mathbf{I}_t) \mathbf{t} - \mathbf{t} \circ \mathbf{t} \), where \(\circ\) denotes the Hadamard (elementwise) product. For the initial state, the variance comes out as 69.5, which gives a standard deviation of 8.3 moves.
Appendix B: The Shape of the Distribution
Perhaps remarkably, we were able to calculate both the mean and the variance of the moves-to-win distribution using the fundamental matrix from the Markov chain. It would however be nice to have some insight into why the distribution is the shape that it is. The approach I'll suggest here is only approximate, but it does match the empirical results from the simulation of the chain quite closely, and it provides some useful insights.
We'll begin by revisiting an observation that we made above: the sum of the tiles on the board increases by either 2 or 4 with each transition (other than the first transition from the initial state). If we were interested in hitting a specific sum for the tiles on the board, rather than hitting a 2048 tile, then it's relatively straightforward to calculate the required number of transitions using the binomial distribution, as we'll see below.
So, the next question is, which sum should we aim to hit? From the Markov chain analysis above, we determined that there are 26 absorbing (winning) states, and we've also seen that they are in different 'sum layers', so there isn't a single target sum — there are several target sums. What we need to know is the probability of being absorbed in each state, which is called an absorbing probability. We can then add up the absorbing probabilities for each of the absorbing states in a particular sum layer to find a probability of winning with a given target sum.
Absorbing Probabilities
Fortunately, the absorbing probabilities can also be found from the fundamental matrix. In particular, we can obtain them by solving the linear equations \[ (\mathbf{I}_t - \mathbf{Q}) \mathbf{B} = \mathbf{R} \] for the \(t \times r\) matrix \(\mathbf{B}\), whose \((i, j)\) entry is the probability of being absorbed in state \(j\) when starting from state \(i\). As before, we are interested in the absorbing probabilities when we start from the initial state. Plotting out the absorbing probabilities, there are 15 absorbing states for which the probabilities are large enough to plot (at least \(10^{-3}\)):
In particular, most games end in either the \(\{2,2,8,8,2048\}\) state, which has sum 2068, or the \(\{2,4,16,2048\}\) state, which has sum 2070. Summing up all of the absorbing states by layer sum gives the complete layer sum probabilities:
Binomial Probabilities
Now that we have some sums to aim for, and we know how often we are aiming for each one, the next question is, how many moves does it take to hit a particular sum? As noted above, we can think of this in terms of the Binomial distribution, which lets us calculate the probability of a given number of "successes" out of a given number of "trials".
In this case, we'll consider a "trial" to be a move, and a "success" to be a move in which the game gives us a 4 tile; as we've seen above, this happens with probability 0.1. A "failure" here is a move in which the game gives us a 2 tile, which happens with probability 0.9.
With this interpretation of successes, in order to hit a given sum \(S\) in \(M\) moves, we need \(\frac{S}{2} - M\) successes out of \(M\) moves. This is because each move counts at least \(2\) toward the sum, which contributes a total of \(2M\), and each success counts an additional \(2\) toward the sum, for a total contribution of \(2 \left(\frac{S}{2} - M\right) = S - 2M\); adding these contributions together leaves the desired sum, \(S\).
The joint probability of obtaining a sum \(S\) in a number of moves \(M\) is then Binomial, and in particular \[ \mathrm{Pr}(M=m, S=s) = B\left(\frac{s}{2} - m; m, 0.1\right) \] where \(B(k; n, p)\) is the probability mass function for the binomial distribution, which gives the probability of exactly \(k\) successes in \(n\) trials, where the probability of success is \(p\), namely \[ B(k; n, p) = {n\choose k}p^k(1-p)^{n-k} \] where \(n \choose k\) denotes a binomial coefficient.
Now if we know the target sum \(S\) that we are aiming for, we can compute the conditional distribution of the number of moves given that sum, which is what we are interested in, from the joint distribution. That is, we can find \(\mathrm{Pr}(M | S)\) as \[ \mathrm{Pr}(M | S) = \frac{\mathrm{Pr}(M, S)}{\mathrm{Pr}(S)}. \] where \(\mathrm{Pr}(S)\) is obtained from the joint distribution by summing out \(M\) for each possible sum \(S\). It's worth noting that \(\mathrm{P}(S)\) is less than one for each possible sum, because there's always a chance that the game 'skips' the sum by placing a 4 tile.
With these conditional distributions for each target sum in hand, we can then add them up, weighted by the total absorbing probability for the target sum, to obtain the overall distribution. This gives a fairly good match to the distribution from the simulation:
Here the simulated distribution is shown with the grey bars, and the colored areas show each of the conditional distributions, which are stacked. Each conditional distribution is scaled according to the total absorbing probability for its sum, and also shifted a few moves, with larger sums requiring more moves on average.
One interpretation of this result is that, if playing optimally, the number of moves to win is essentially determined by how quickly the player can get to a sum large enough to have a 2048 tile, which is in turn governed by the number of 4 tiles, which follows a binomial distribution.
Thanks to Hope Thomas and Nate Stemen for reviewing drafts of this article.
If you've read this far, perhaps you should follow me on twitter, or even apply to work at Overleaf. :)
Source: https://jdlm.info/articles/2017/08/05/markov-chain-2048.html
0 Response to "How to Continuously Move in 2048"
Post a Comment